Hace mucho tiempo en la inhóspita blogosfera una panda de frikis creó Sospechosos Habituales. Desde aquel fatídico día nadie está libre de sospecha. No trates de disimular, si vienes mucho por aquí tu también serás un... Sospechoso Habitual
31 mayo 2007
Gadget: música en la ducha
Un buen amigo mío me regaló (a cambio de algunos puntos) esta fantástica radio resistente a la ducha. Mis momentos de higiene han mejorado mucho desde entonces. Es perfecta. Etiquetas: tecnología
Sospechoso:
Fichado a las: 20:08
xxxxx
Certeza
Los Matemáticos dominaremos el mundo (algún día) Etiquetas: humor, matemáticas
Otra tira cojonuda de la xkcd.
Sospechoso:
Fichado a las: 17:23
xxxxx
30 mayo 2007
Relatos de Sant Jordi 2007 (II)
Etiquetas: librosOrigami, una fábula.
Origami es el arte japonés de doblar papel. O al menos eso era lo que decía Carlos siempre que alguien lo pillaba enfrascado en su afición.
Carlos doblaba todo papel que tuviese a mano. Propaganda, borradores e incluso algún que otro documento importante podían verse transformados en una variada gama de figuritas si se le acercaban demasiado. Además era algo que hacía en cualquier sitio.
Sus profesores ya conocían todo su repertorio y no eran pocos los usuarios de la linea de tren que solía usar que no lo hubiesen visto alguna vez dando forma a un cuadradito de papel con cara de concentrado.
Así empieza el relato con el que no gané ningún premio de narrativa de los Juegos Florales que se organizaron en mi facultad el pasado Sant Jordi.
Si quieren saber cómo acaba bájense el PDF.
Sospechoso:
Fichado a las: 09:08
xxxxx
29 mayo 2007
Relatos de Sant Jordi 2007 (I)
Etiquetas: librosEl estrangulador topológico.
Érase una vez un hombre malvado, un pusilánime de negro corazón, un asesino cruel y despiadado cuya mente enajenada disfrutaba estrangulando jovencitas indefensas. Esta es la historia de su infame existencia.
Miguel era de día una persona normal. Bueno, todo lo normal que puede ser un profesor de matemáticas. Sin embargo, cada noche, llevado por una oscura fuerza caía en un terrible frenesí homicida.
Siguiendo sus impulsos salía a la calle ataviado con una larga gabardina de color pardo y un sombrero de fieltro marrón dispuesto a acabar con la vida de su siguiente víctima.
Así empieza el relato con el que gané el primer premio de narrativa de los Juegos Florales que se organizaron en mi facultad el pasado Sant Jordi.
Si quieren saber cómo acaba bájense el PDF.
Sospechoso:
Fichado a las: 08:56
xxxxx
28 mayo 2007
Loosing our Religion
Una pequeñísima selección de las frases sobre religión que encontré en Desvariandoando: -Abu´l-Ala-Al-Ma´arri- -Woody Allen cineasta estadounidense- -Anónimo- -Anónimo- -Anónimo- -San Agustín de Hipona Padre de la Iglesia- -Santo Tomás de Aquino- -Santo Tomás de Aquino- -Isaac Asimov escritor y bioquímico estadounidense- -Mikhail A. Bakunin anarquisa ruso- -Mikhail A. Bakunin anarquisa ruso- -Mikhail A. Bakunin anarquisa ruso- -Dan Barker ex-predicador- - -Jorge Luis Borges escritor argentino- -Jorge Luis Borges escritor argentino- -Chapman Cohen- -Noam Chomsky- -Richard Dawkins- -Tyler Durden (El club de la lucha)- -Philip K. Dick- -Sigmund Freud- -Stephen W. Hawking- -Sherlock Holmes (Sir Arthur Conan Doyle), "Un Escándalo en Bohemia"- -Laplace- -Karl Marx- -Friedrich Wilhelm Nietzsche- -Friedrich Wilhelm Nietzsche- -Friedrich Wilhelm Nietzsche- -Friedrich Wilhelm Nietzsche- -Stephen F. Roberts- -Carl Sagan astrónomo estadounidense 1934-1996- -Voltaire- -Voltaire- Etiquetas: citas, reflexionesEn el mundo existen dos clases de hombres: hombres inteligentes sin religión y hombres religiosos sin inteligencia.
Para TI yo soy un ateo, para Dios soy la Oposición Leal.
Si te enseñaran que los duendes causan la lluvia, cada vez que lloviera, verías las pruebas de que existen los duendes.
Reza lo que te de la gana pero no dejes de remar hacia la orilla.
La única iglesia que ilumina es la que arde.
El buen cristiano debe permanecer alerta de los matemáticos y todos aquéllos que realicen profecías vacías. Ya existe el peligro de que los matemáticos hayan hecho una alianza con el Demonio para oscurecer el espíritu y confinar al hombre en las ataduras del Infierno.
No es evidente que dios exista.
Ten cuidado con el hombre de un solo libro.
Examinen fragmentos de pseudociencia y encontrarán un manto de protección, un pulgar que chupar, unas faldas a las que agarrarse. Y, ¿qué ofrecemos nosotros a cambio? ¡Incertidumbre! ¡Inseguridad!
Todas las religiones, con sus dioses, semidioses, profetas, mesías y santos son el producto del capricho y la credulidad del hombre quien no ha alcanzado todavía el desarrollo total y la personalidad completa de sus poderes intelectuales.
Me atrevo a cambiar la frase de Voltaire para decir que, preferiblemente, si Dios realmente existiera, sería necesario abolirlo.
La religión es demencia colectiva.
La verdad no demanda creencias. Los científicos no unen sus manos cada domingo, cantando '¡Sí, la gravedad es real! ¡Tendré fe! ¡Seré fuerte! Creo en mi corazón que lo que sube tiene que bajar. ¡Amén!'. Si lo hicieran, pensaríamos que están bastante inseguros de ello.
Sí Jesús hubiera sido ejecutado hace veinte años, los niños católicos irían a la escuela con sillitas eléctricas en sus cuellos en lugar de cruces.
Lenny Bruce-Dios mueve al jugador y éste la pieza ¿Qué Dios detrás de Dios la trama empieza?
Israelitas, cristianos y musulmanes profesan la inmortalidad, pero la veneración que tributan al primer siglo prueba que sólo creen en él, ya que destinan todo lo demás, en número infinito, a premiarlo o castigarlo.
Los dioses son cosas frágiles; pueden ser asesinados con un atisbo de ciencia o una dosis de sentido común.
Si no creemos en la libertad de expresión para aquellas personas que despreciamos, entonces no creemos en ella para nada.
Todos somos ateos respecto a la mayoría de dioses en los que la humanidad ha creído alguna vez. Algunos de nosotros simplemente vamos un dios más allá.
¡Yo no sé nada de Dios! Cuando éramos niños, nuestros padres eran nuestros modelos de Dios. Y si nuestros padres nos decepcionaron, ¡¿qué nos dice eso de Dios?!
La realidad es aquello que, cuando dejas de creer en ella, no desaparece.
La religión es comparable con la neurosis infantil.
Lo que he hecho es mostrar que es posible que la forma en que comenzó el universo esté determinada por las leyes de la ciencia. En ese caso, no sería necesario apelar a Dios para decidir cómo comenzó el universo. Esto no prueba que no exista dios, sólo que Dios no es necesario.
Es un error capital el teorizar antes de poseer datos. Insensiblemente uno comienza a alterar los hechos para encajarlos en las teorías, en lugar encajar las teorías en los hechos
Yo afortunadamente no tengo la necesidad de creer en dios.
La religión es el opio del pueblo.
El último cristiano murió en la cruz.
Los Grandes Intelectos son escépticos.
Fe: no querer saber la verdad.
No puedo creer en un Dios que quiera ser alabado todo el tiempo.
Yo digo que ambos somos ateos. Yo sólo creo en un dios menos que tu. Cuando entiendas porqué tu deshechas todos los otros posibles dioses, entonces entenderás porqué yo deshecho el tuyo.
No puedes convencer a un creyente de nada porque sus creencias no están basadas en evidencia, están basadas en una enraizada necesidad de creer.
La duda no es una condición placentera pero la certeza es absurda.
El ateísmo es el vicio de unas pocas personas inteligentes.
Sospechoso:
Fichado a las: 10:34
xxxxx
27 mayo 2007
Maratón de Problemas Primavera 2007
Señoras y señores, hasta aquí llegó la Primera Maratón de Problemas de Sospechosos Habituales. Etiquetas: matemáticas, metasospechosos
Por mi parte les diré que estoy gratamente sorprendido de la cantidad y la calidad de los participantes. Quisiera pedirles ahora (a los que han participado y a los que no) que pot favor sigan participando en este blog, aportando su punto de vista en los comentarios.
Pero bueno, me dejo de rollos y voy al grano: Lista de Problemas
Y también... El Ránking final
¡Felicidades a todos y en especial a Nabil que ha ganado después de currarse 14 soluciones correctas!
Espero que se hayan divertido tanto como yo y que vuelvan a participar en la próxima.
PD: Por supuesto están todos invitados a dejar su opinión en los comentarios sobre el nivel de dificultad, la temática de los problemas o cualquer otro tema relacionado con esta Maratón.
Sospechoso:
Fichado a las: 18:08
xxxxx
Solución al problema XV
La solución al Problema XV es: Etiquetas: matemáticas
El secreto para resolver este problema consiste en darse cuenta de que sobre el mismo tablero han tenido lugar dos partidas independientes, una sobre casillas blancas y otra sobre casillas negras.
Una vez visto eso hay que intentar reconstruir la última jugada. Por ejemplo, en las casillas blancas la última jugada la puede haber hecho el Rey negro o el Alfil blanco si es que el Alfil blanco va por casillas blancas. En las casillas negras sin embargo no tenermos tantas opciones. Los Peones blancos no han movido (pues están en sus casillas de origen y no pueden retroceder) y el Rey blanco tampoco (porque los Peones le tapan el paso y si hubiese enrrocado no hubiese podido volver a su casilla de salida), así que ningúna de esas tres fichas ha podido hacer el último movimiento sobre las casillas negras. Así pues el único que se ha podido mover por las casillas negras es el Alfil.
Conclusión: el Alfil blanco se mueve por las casillas negras.
El Ranking va así:
Sospechoso:
Fichado a las: 18:05
xxxxx
Big Girls (You Are Beautiful)
Este chico me tiene loquita. Y más con este himno-homenaje a todas nosotras. Un exitazo. Etiquetas: música, personal, publicidad, reflexionesYou take your girl and multiply her by four
Now a whole lot of woman needs a whole lot more
Porque, la verdad, no hay que vivir acomplejado. Y parece que, aunque sea sólo una estrategia de márketing, ahora se está poniendo de moda hacer promociones con mujeres no-esqueléticas. Como ésta, la más famosa que nos viene a la cabeza (aquí, la versión argentina).
Cuando salió por televisión por primera vez, me di cuenta de que a mis amigos, primos, etc. no les gustaban las modelos de talla 36 tanto como creía, y sobre todo, que el "que tenga por dónde agarrarla" era una virtud y no un defecto.
Así que ya sabéis: Big Girls, somos bonitas.
Habló una big girl preciosa.
Sospechoso:
Fichado a las: 01:15
xxxxx
26 mayo 2007
Maratón de Problemas XV
La extraña partida: Etiquetas: matemáticas
ACTUALIZACIÓN: Había una frase en el enunciado que podía inducir a error, La he eliminado, por favor vuelvan a leer el enunciado con atención. Ojo que el enunciado se las trae:
En la imagen superior pueden ver un tablero de ajedrez con los dos Reyes señalados con una R (cada una de su respectivo color) y un par de peones blancos señalados con una P. La partida que se ha disputado en ese tablero es de lo más extraña. Pese a seguir al pie de la letra todas las reglas del ajedrez los jugadores (cachondos ellos) han decidido añadir una nueva regla para hacerla más interesante. Se trata de una partida monocromática.
Para el que no conozca ese tipo de partidas diré que son unas partidas normales a excepción de la regla de monocromía: Si una pieza (sea esta del color que sea) empieza sobre una casilla de color blanco, sólo podrá moverse por casillas de color blanco. De la misma manera una pieza que empiece en una casilla de color negro sólo podrá moverse por casillas negras.
Si reflexionan un poco se darán cuenta de que estó tiene ciertas consecuencias inmediatas. Por ejemplo, los caballos no pueden moverse, así que han sido comidos en sus mismas casillas de salida. El enroque largo queda prohibido por esa norma y tanto el Rey, como la Reina, la Torre y los Peones ven reducida su movilidad. Al único que parece no importarle el tema monocromático es al Alfil, que puede moverse y matar como siempre.
Y precisamente es del alfil del que quiero hablar. Si se fijan bien verán que en el conteo se marcan 4 piezas blancas y en el tablero sólo hay 3. La que falta es un Alfil blanco que por accidente se ha salido del tablero. ¿Me podría decir, querido lector, si ese Alfil se movía por casillas blancas o por casillas negras?
AVISO: Este es el último problema, mañana después de publicar la solución publicaré el ranking definitivo y un repaso-resumen de la Maratón.
Si quieren participar en esta maratón de problemas lean las instrucciones que aparecen en el primer problema.
Sospechoso:
Fichado a las: 17:59
xxxxx
Solución al problema XIV
La solución al Problema XIV es: Etiquetas: matemáticasEn contra de lo que parece a primera vista la repartición correcta no es Pedro 5 monedas - Felipe 3 monedas sinó Pedro 7 monedas - Felipe 1 moneda. Veamos porqué:
Cada cual se come 8/3 de huevo en su ración de tortilla, así que Saturnino ha pagado 8 monedas por sus 8/3 de huevo de donde cada huevo vale 3 de monedas. Ahora bien, Pedro puso 5 huevos y se comió 8/3 de huevo por lo tanto puso 15/3-8/3=7/3 de huevo de más. De la misma manera calculamos que, si Felipe puso 3 huevos y se comió 8/3 de huevo, puso 9/3-8/3=1/3 de huevo de más.
Así pues, multiplicando esas cantidades por las 3 monedas que vale cada huevo sale que Pedro tiene que llevarse 7 monedas y Felipe sólo 1.
El Ranking va así:
Sospechoso:
Fichado a las: 17:57
xxxxx
25 mayo 2007
Maratón de Problemas XIV
/* Siento el retraso, problemas varios */ Etiquetas: matemáticas
Los huevos de los excursionistas:Pedro, Felipe y Saturnino van de excursión. A la hora de comer deciden, para mayor comodidad, preparar un plato único reuniendo las provisiones de los tres. Como tienen muchos huevos, deciden hacer una tortilla, que se repartirán a partes iguales. Pedro aporta 5 huevos y Felipe 3.
-Yo no tengo huevos -dice Saturnino- así que pondré dinero. Tomad 8 monedas.
¿Cómo deben repartirse Pedro y Felipe las 8 monedas?
AVISO: Mañana sábado SI habrá problema y de hecho será el último (problema número XV) El domingo a media tarde publicaré el ránking definitivo.
Si quieren participar en esta maratón de problemas lean las instrucciones que aparecen en el primer problema.
Sospechoso:
Fichado a las: 20:49
xxxxx
Solución al problema XIII
La solución al Problema XIII es: Etiquetas: matemáticas31, la serie consiste en escribir el número 16 en diferentes bases empezando por 16 en base 16 (=10) y acabando por 16 en binario (=10000). El interrogante se corresponde con 16 en base 5, que es 31.
El Ranking va así:
Sospechoso:
Fichado a las: 20:47
xxxxx
Psicohistoria y patentes...
-Hari Seldon- Etiquetas: citasLa suma del saber humano está por encima de cualquier hombre; de cualquier número de hombres.
Sospechoso:
Fichado a las: 14:28
xxxxx
Día del orgullo Friki 2007
Interrumpimos brevemente la Maratón de Problemas para recordar a todos los lectores que hoy es... Etiquetas: friki
Así que no salgan de casa sin su toalla y estén atentos a sus blogs frikis favoritos.
Algo de culturilla: El día del Orgullo Friki se celebra en 25 de Mayo para conmemorar el estreno de Star Wars (A New Hope). Pues bien, este año se celebran exactamente 30 años de ese estreno así que me ahí va mi humilde homenaje: Star Wars Kid, 3 versiones
PD: No dejen de visitar la sección Star Wars de Nopuedocreer.
Sospechoso:
Fichado a las: 10:14
xxxxx
24 mayo 2007
Maratón de Problemas XIII
Monotonía: Etiquetas: matemáticasEn esta sucesión (de lo más repetitiva, por cierto) falta un número. ¿Cual es?
10, 11, 12, 13, 14, 15, 16, 17, 20, 22, 24, ?, 100, 121, 10000
Nota: NO es fácil.
AVISO: Este sábado SI habrá problema y de hecho será el último (problema número XV) El domingo a media tarde publicaré el ránking definitivo. No desfallezcan que sólo quedan 2 más.
Si quieren participar en esta maratón de problemas lean las instrucciones que aparecen en el primer problema.
Sospechoso:
Fichado a las: 15:58
xxxxx
Solución al problema XII
La solución al Problema XII es: Etiquetas: matemáticasTan sólo había que fijarse en que:
Es decir, que las potencias de 7 repiten la cifra final tras un ciclo de 4 elementos 1=>7=>9=>3=>1=>... lo que quiere decir que 7^(4n+k) mod 10 =7^k mod 10 para todo n natural.
Así pues calculamos: 83579 mod 4 = 3 e immediatamente sabemos que 7^83579 mod 10 = 7^3 mod 10 = 3
Nota: La operación X mod Y consiste en hacer la división entera X/Y y quedarse con el resto. En nuestro caso X mod 10 el resultado es la última cifra del número.
El Ranking va así:
Sospechoso:
Fichado a las: 15:54
xxxxx
23 mayo 2007
Maratón de Problemas XII
Un problema potente: Etiquetas: matemáticas¿En qué cifra acaba el número 7^83579?
Nota: X^Y significa "X elevado a Y".
Nota: Obviamente hay que justificar la solución sin usar ningún tipo de calculadora (no se vale un: "he programado el ordenador para que lo calcule" o un "Maple/Mathematica/Matlab/la Calculadora de Windows dice que...").
AVISO: Este sábado SI habrá problema y de hecho será el último (problema número XV) El domingo a media tarde publicaré el ránking definitivo. No desfallezcan que sólo quedan 3 más.
Si quieren participar en esta maratón de problemas lean las instrucciones que aparecen en el primer problema.
Sospechoso:
Fichado a las: 15:40
xxxxx
Solución al problema XI
La solución al Problema XI es: Etiquetas: matemáticas
4R+2r. Veamos porqué: Al ser el triángulo rectángulo su hipotenusa AC es un diámetro de la circumferencia. Por lo tanto AC mide 2R. Por otro lado es obvio que AE=AF y que CD=CE de donde AF+CD=AE+EC=AC que mide 2R. Ahora sólo nos queda contar lo que mide BF+BD, pero resulta que el triángulo es rectángulo y la circumferencia pequeña (de radio r) es tangente a los dos catetos lo cual significa que el centro de esta, dos radios y los dos segmentos de catetos citados forman un cuadrado, es decir, BF=BD=r. Así pues BF+BD=2r.
Resumiendo, el perímetro es igual a 4R+2r.
El Ranking va así:
Sospechoso:
Fichado a las: 15:38
xxxxx
22 mayo 2007
Maratón de Problemas XI
La suma de los Catetos: Etiquetas: matemáticasUno "sencillo": Tenemos un triángulo rectángulo y sus respectivos círculos inscrito y circumscrito. Sabemos que el radio de ambos círculos es r y R respectivamente y nos gustaría saber cual es el perímetro del triángulo.
Este problema tiene una solución taaaaan elegante que habría que publicarla en el BOE.
Si quieren participar en esta maratón de problemas lean las instrucciones que aparecen en el primer problema.
Sospechoso:
Fichado a las: 15:58
xxxxx
Solución al problema X
La solución al Problema X es: Etiquetas: matemáticasEn realidad hay 26 posibles respuestas y sus respectivas simétricas, en particular tenemos esta: 17125623475364
El Ranking va así:
Sospechoso:
Fichado a las: 15:56
xxxxx
21 mayo 2007
Meme: escucho, veo y juego. Las cosas en mi PC.
¡Alexliam y austerhouse me han mandado un meme! Sólo he tenido que darles una leve indirecta para que lo hicieran jejeje. Bien, la broma consiste en contestar cuatro cositas: Etiquetas: memes
Reproductor de música / video / DVD:
iTunes o WinAmp (iPod en el tren)/ WinAmp / DVD de la tele
Número de MP3s en tu Mac o PC:
2854
Número de películas descargadas:
Una, para regalársela a Sete, porque el DVD está descatalogado.
Número de DVD originales:
La colección entera de cine español de El País. Comprados, 20 o 25.
Número de series que estás descargando:
Daria. Pero ya hace años que intento descargarla entera y de momento sólo he conseguido dos temporadas.
Número de animes que estás descargando:
Ninguno.
Número de series que ya has descargado:
Ninguna.
Número de juegos de PC/Mac que tienes:
Unos cuantos, 25 o 30, acumulados desde la niñez.
Juego al que estás enganchado últimamente:
Del PC ninguno, pero cuando terminen los exámenes pienso recuperar activamente mi Sega Mega Drive. Especialmente el juego de Sonic.
Hay que decir que todos mis DVD, CD's (casi 500),etc. son tanto míos como de mis padres, porque parece extraño pero tenemos mil gustos en común.
Mil besos para los remitentes del meme. Me encantan los memes.
Sospechoso:
Fichado a las: 23:28
xxxxx
Maratón de Problemas X
14 Fichas Etiquetas: matemáticasTenemos 14 fichas numeradas del 1 al 7 (cada número aparece en dos fichas). Queremos ordenarlas de forma que entre los dos 1 haya una ficha, entre los dos 2 haya dos fichas, entre los dos 3 haya tres fichas, etc. ¿Es posible ordenarlas así? ¿Es única esta ordenación?
Nota: las fichas están en fila. No se vale ponerlas en círculo ni en ninguna otra formación rara. (Que os conozco!)
Si quieren participar en esta maratón de problemas lean las instrucciones que aparecen en el primer problema.
Sospechoso:
Fichado a las: 13:20
xxxxx
20 mayo 2007
Jugar X Jugar (objetivo conseguido)
Objetivo conseguido: Etiquetas: juegos
El viernes me escapé un rato a la feria JugarXJugar de Granollers y estuve charlando con Oriol Comas Coma (que me firmó su libro y me enseñó un par de juegos) y con algunos de los foreros de la BSK (que obviamente estaban jugando).
La feria en sí no está mal del todo, sobretodo teniendo en cuenta que es la primera edición de una feria dedicada a un tema tan poco popular como son los juegos. Faltaba mucho sector empresarial y quizás también algo de información. Claro que lo primero se solucionará con el tiempo (y precisamente gracias a este tipo de eventos) y lo segundo quedaba suplido por el montón de jugones que había allí (BSK y en especial Comas a la cabeza).
En fin, espero que repitan el año que viene y espero poder visitarla con más calma.
Sospechoso:
Fichado a las: 00:13
xxxxx
19 mayo 2007
Solución al problema IX
La solución al Problema IX es: Etiquetas: matemáticas
En el dibujo (que he robado a Nabil porque el mio era más cutre) están marcadas las 4 partes.
El lunes cuelgo el próximo problema.
El Ranking va así:
Sospechoso:
Fichado a las: 18:28
xxxxx
How-To: La misteriosa mutación de unas alpargatas Victoria
cus·tom·ize
tr.v. cus·tom·ized, cus·tom·iz·ing, cus·tom·iz·es
To make or alter to individual or personal specifications: customize a van.
El primer paso para crear es tener el material: pinturas acrílicas.
También se necesita una víctima a la que aplicar el material.
Hay que pintar el fondo y dejar toda la noche que se seque bien.
Luego ya se pueden ornamentar. Aquí interviene la mano paterna.
Hay que cuidar los detalles.
Se dejan secar y... listas para triunfar.
Sospechoso:
Fichado a las: 16:55
xxxxx
18 mayo 2007
Maratón de Problemas IX
Divide y vencerás: Etiquetas: matemáticasQueremos dividir un tablero de ajedrez en cuatro partes iguales de forma y tamaño de manera que cada una de las partes tenga más del doble de las casillas de un color que de otro. Es decir, queremos que dos partes tengan más del doble de sus casillas blancas y que las otras dos tengan más del doble de sus casillas negras. Para ello no podemos dividir casillas, ni eliminar trozos y además sólo se considerarán "unidas" dos casillas que tengan todo un lado en común.
Si quieren participar en esta maratón de problemas lean las instrucciones que aparecen en el primer problema.
Sospechoso:
Fichado a las: 16:05
xxxxx
Solución al problema VIII
La solución al Problema VIII es: Etiquetas: matemáticasEn contra de lo que parece a simple vista no son 11 sino tan sólo 7 las pesadas necesarias. Veamos el procedimiento:
Se divide el conjunto en tres partes más o menos iguales (682+683+683). Se comparan las dos partes que tengan el mismo número de monedas y entonces, si la balanza se equilibra la moneda estará en el otro grupo mientras que si no se equilibra estará en el grupo que pese menos. Repitiendo el proceso con el grupo donde sabemos que está la moneda podremos encontrar en 7 pesadas la misma dado que en el peor de los casos el tamaño de los grupos será: 2048 => 1º => 683 => 2ª => 228 => 3º => 76 => 4º => 26 => 5º => 9 => 6º => 3 => 7ª => 1
El Ranking va así:
Sospechoso:
Fichado a las: 16:03
xxxxx
17 mayo 2007
Maratón de Problemas VIII
La falsa moneda: Etiquetas: matemáticasTenemos 2048 monedas aparentemente iguales. Sabemos sin embargo que hay una que es falsa y pesa un poco menos que las demás y queremos encontrarla. Para ello disponemos de una balanza de dos platillos con la que comparar monedas entre sí. La balanza es muy precisa y en cada platillo caben todas las monedas que haga falta. ¿Cual es el número mínimo de pesadas que se necesitan para determinar sin ninguna duda cual es la falsa moneda? ¿Cómo lo harían?
Si quieren participar en esta maratón de problemas lean las instrucciones que aparecen en el primer problema.
Nota: Mañana publicaré la respuesta un poco antes de lo habitual (entre las 13 y las 14 h) así que no se duerman.
Sospechoso:
Fichado a las: 16:12
xxxxx
Solución al problema VII
La solución al Problema VII es: Etiquetas: matemáticasDado que un cliente se lleva X litros y el otro 2X tenemos que encontrar 5 barriles tales que la suma de sus capacidades sea igual a 3X. En particular la suma de sus capacidades debe ser múltiplo de 3.
Si dividimos las 6 capacidades: 15, 16, 18, 19, 20 y 31 entre 3 y nos quedamos con sus respectivos restos tenemos: 0, 1, 0, 1, 2 y 1 respectivamente. Ahora tenemos que escoger 5 de esas cantidades de manera que sumadas den 0 o múltiplo de 3. No es difícil ver a ojo que cogiendo todos los barriles menos el penúltimo se cumple la condición (0+1+0+1+1=3) de manera que este debe ser el de cerveza.
Por lo tanto el bodeguero tiene 20 litros de cerveza.
El Ranking va así:
PD: Últimamente hay algunos problemas en la recepción de mails así que no se asusten si las puntuaciones bailan un poco de un día para otro. Estén atentos y avísenme de cualquier incidencia y procuraré corregir los fallos.
Sospechoso:
Fichado a las: 16:10
xxxxx
16 mayo 2007
Maratón de Problemas VII
El barril de cerveza: Etiquetas: matemáticasUn bodeguero tiene 5 barriles de vino y uno de cerveza. A primera hora de la mañana vende una determinada cantidad de vino a un cliente y poco más tarde vende el doble de esa cantidad a otro, momento en el cual se queda sin vino. Ahora bien, si sabemos que el vino lo vende siempre por litros enteros y que las capacidades de los barriles son 15, 16, 18, 19, 20 y 31 litros (no necesariamente en ese orden)... ¿Cuantos litros de cerveza tiene el bodeguero?
Nota: Los cliente vienen a buscar el vino con sus propios envases, no es necesario que se lleven un barril entero.
Nota2: Los barriles estan llenos al principio de la historia.
Si quieren participar en esta maratón de problemas lean las instrucciones que aparecen en el primer problema.
Sospechoso:
Fichado a las: 15:54
xxxxx
Solución al problema VI
La solución del Problema VI es: Etiquetas: matemáticas
El Ranking va así:
Sospechoso:
Fichado a las: 15:52
xxxxx
15 mayo 2007
Jugar X Jugar
Este viernes por la tarde me dejaré caer un rato por la Feria Jugar x Jugar de Granollers. Es la primera edición y no se exactamente qué encontraré, pero sabiendo que la organiza Oriol Comas Coma y que va de juegos de mesa estoy seguro de que disfrutaré como un enano (y nunca mejor dicho). Etiquetas: actualidad, curiosidades, juegos
Así pues, lo dicho, si alguien quiere que le firme algún autógrafo que esté atento porque estaré poco rato e iré por faena.
Yo por mi parte intentaré que Oriol me firme su libro!
Sospechoso:
Fichado a las: 16:11
xxxxx
Maratón de Problemas VI
Estrellas Trianguladas: Etiquetas: matemáticas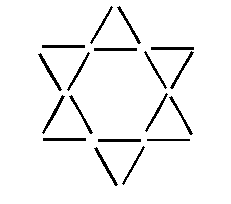
En la imagen pueden ver una figura compuesta por 18 palillos en la que se pueden apreciar 8 triángulos equiláteros (6 pequeños y 2 grandes). ¿Son capaces de crear una nueva figura en la que se aprecien solamente 6 triángulos equiláteros moviendo 2 palillos?
Nota: no vale añadir o quitar palillos, tan sólo se pueden mover 2.
Nota2: la figura tiene que se "cerrada" es decir, tiene que estar formada por una unión de polígonos. No pueden quedar palillos sueltos o "antenas".
Si quieren participar en esta maratón de problemas lean las instrucciones que aparecen en el primer problema.
Sospechoso:
Fichado a las: 16:09
xxxxx
Solución al problema V
La solución al Problema V es: Etiquetas: matemáticasLlamemos X al número que buscamos, entonces sabemos que X+1 es el entero positivo más pequeño divisible por 1, 2, 3, 4, 5, 6, 7, 8 y 9. Es decir, X+1 es el Mínimo Común Múltiplo de todos esos números. Así pues calculamos: X+1 = MCD(1,2,3,4,5,6,7,8,9) = 8*9*7*5 = 2520. De donde X = 2519.
El Ranking va así:
Sospechoso:
Fichado a las: 16:07
xxxxx
14 mayo 2007
Maratón de Problemas V
Mínimo Común (No) Múltiplo: Etiquetas: matemáticasEncuentra el menor de los enteros positivos tal que al dividirlo por:
Si quieren participar en esta maratón de problemas lean las instrucciones que aparecen en el primer problema.
Sospechoso:
Fichado a las: 11:03
xxxxx
¡Mi foto!
Papá Oso ya nos enseñó la suya. Ahora me toca a mí. Ésta es la foto que he mandado al grupo Flickr24h. Sí, el 5 de mayo estuve tocando en una iglesia. Etiquetas: fotografía
Sospechoso:
Fichado a las: 10:00
xxxxx
13 mayo 2007
Answering
-Woody Allen- Etiquetas: citas, reflexiones, sexoLove is the answer, but while you're waiting for the answer, sex raises some pretty interesting questions
Vía: La lista de Correo de El Listo.
Sospechoso:
Fichado a las: 11:15
xxxxx
12 mayo 2007
Solución al problema IV
La solución al Problema IV es: Etiquetas: matemáticas
Y por lo visto era difícil porque sólo han contestado 3 personas. En todo caso que conste en acta que me he cortado, porque en la maratón de verdad tenían que hacer desde la 2x2 hasta la 8x8.
AVISO: Durante el fin de semana no habrá nuevos problemas para no perjudicar a aquellos que no puedan conectarse.
El Ranking va así:
Sospechoso:
Fichado a las: 16:30
xxxxx
11 mayo 2007
Maratón de Problemas IV
Los Putos Puntos: Etiquetas: matemáticas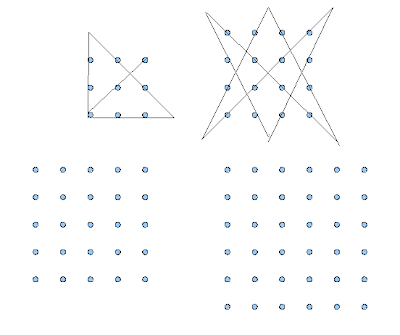
Tenemos cuatro cuadrículas de 3x3, 4x4, 5x5 y 6x6 puntos (respectivamente). Queremos unir los puntos de cada cuadrícula con una única linea poligonal continua que pase por todos ellos. Los ejemplos sencillos con 3x3 y 4x4 puntos ya están resuletos. ¿Se atreven con los casos 5x5 y 6x6?
Tengan en cuenta que las líneas poligonales deben ser cerradas como en el caso 4x4 en vez de abiertas como en el caso 3x3. Tengan en cuenta también que se puede cruzar una linea pero no recorrerla dos veces.
ACTUALIZACIÓN: Como bien apuntan en los comentarios NO se puede usar qualquier cantidad de lineas!!! Para el 5x5 pueden usar 8 rectas y para el 6x6 pueden usar 10 rectas. En ningún caso más (si alguien lo saca con menos estaré encantado de verlo).
Si quieren participar en esta maratón de problemas lean las instrucciones que aparecen en el primer problema.
Sospechoso:
Fichado a las: 15:36
xxxxx
Solución al problema III
La solución al Problema III es la siguiente: Etiquetas: matemáticas
Si en llenar una caja tardamos N minutos, en llenar media tardaremos N-1 porque cada minuto doblamos el número de pelotitas que hay en la caja:
Minuto 0 = 1 Pelotita (la "muestra")
Minuto 1 = 2 Pelotitas (la "muestra" y la primera que ha hecho)
Minuto 2 = 4 Pelotitas (la "muestra", la que ha hecho en el minuto 1 y las dos que acaba de hacer)
etc...
El Ranking va así:
Sospechoso:
Fichado a las: 15:34
xxxxx
Mozart en un momento
Hace unos días descubrí este vídeo, hecho a partir de secuencias de la película Amadeus. Es realmente genial. Para mí resume toda la vida, la música, el sentimiento que transmite Mozart en sus obras. No dejéis de mirarlo. Subid bien los altavoces.
Sospechoso:
Fichado a las: 11:05
xxxxx
10 mayo 2007
Maratón de Problemas III
Las pelotitas de Ping-Pong: Etiquetas: matemáticasTenemos una máquina muy especial. Se trata de una máquina que fabrica exponencialmente. Es decir: en el primer minuto fabrica 1 objeto, en el segundo minuto 2, en el tercero 4, en el cuarto 8, en el quinto 16, etc... Para que funcione hemos de colocar el objeto que queremos fabricar en un recipiente y a partir de ahí ella sola se pone a crear copias como una loca. Como tenemos una visión comercial muy avanzada decidimos fabricar Pelotitas de Ping-Pong de Color Rosa™ (si, ríanse, pero son el futuro!). Al principio vendíamos las Pelotitas de Ping-Pong de Color Rosa™ en cajas de M unidades pero por motivos de márketing nos indican que deberíamos venderlas en cajas de M/2 unidades. Si antes tardábamos N minutos en llenar una caja de las grandes, ¿cuánto tardaremos ahora en llenar una de las pequeñas?
Si queréis participar en esta maratón de problemas leed las instrucciones que aparecen en el primer problema.
Sospechoso:
Fichado a las: 15:55
xxxxx
Solución al problema II
La solución al problema II consiste en colocar 9 bolas tal y como muestra el siguiente diagrama: Etiquetas: matemáticas
Donde cada cuadrado representa un "piso" del "cubo" (no importa en que orden)
El Ranking va así:
Sospechoso:
Fichado a las: 15:53
xxxxx
09 mayo 2007
Maratón de Problemas II
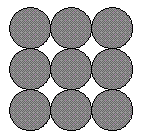
Y vamos con el segundo problema de la Maratón de Problemas de Sospechosos Habituales: El Logo de la UPC Etiquetas: matemáticas
En la imagen superior pueden ver el Logo de la UPC. El problema de hoy trata sobre él y creo que será más difícil de explicar que de resolver:Queremos crear un logotipo tridimensional de la UPC. Esto es una figura tridimensional tal que la mires por donde la mires (por delante, detrás, encima, debajo, derecha e izquierda) tiene la pinta del Logo de la UPC. Para hacerlo empezamos con un "cubo" de 3x3x3 bolas. Esta figura, evidentemente, cumple la condición pero gasta 27 bolas y la verdad es que somos bastante rácanos (Catalanes y tal...) así que nos gustaría hacerlo con menos. Podemos, por ejemplo, quitar la bola "central" porque la figura resultante (un cubo con el interior vacío) también cumple las condiciones. Podemos así mismo quitarle cualquier otra bola y se seguiría viendo el Logo por los 6 lados. Teniendo en cuenta que las bolas pueden quedar "flotando en el aire"... ¿Cual es el número mínimo de bolas necesarias para realizar nuestra figura y cómo las colocarías?
Si queréis participar en esta maratón de problemas leed las instrucciones que aparecen en el primer problema.
PD: En las Maratones de Problemas de la UPC SIEMPRE aparece un problema relacionado con el Logo de la UPC. Digamos que es un clásico.
Sospechoso:
Fichado a las: 16:23
xxxxx
Solución al problema I
// Siento el retraso, el volumen de respuestas ha superado todo lo esperado. Etiquetas: matemáticas
La solución al problema I es:
Se trata de plantear las ecuaciones correctamente:Llamemos V a la velocidad del coche, AB (=10A+B) al primer punto, BA (=10B+A) al segundo y A0B (=100A+B) o B0A (=100B+A) al tercero.
Entonces, sabemos que V=(10B+A)-(10A+B) porque es la distancia que recorre en la primera hora.
Sabemos así mismo que V=(100A+B)-(10B+A) o bien V=(100B+A)-(10B+A) porque es la distancia que recorre en la segunda hora.
Probemos con una de las dos hipótesis: (10B+A)-(10A+B)=V=(100B+A)-(10B+A)
De donde: 10B-B-100B+10B = -81B = A-A-A+10A = 9A
De donde: -9B = A
Cosa que no tiene sentido porque tanto A como B deben ser positivos.
Así pues la hipótesis correcta debe ser: (10B+A)-(10A+B)=V=(100A+B)-(10B+A)
De donde 10B-B-B+10B = 18B = 100A-A-A+10A = 108A
De donde B = 6A y como A y B tienen una sola cifra la única solución es: A = 1 y B = 6
Por lo tanto, la velocidad es 45 Km/h y los puntos kilométricos son: 16, 61 y 106 (respectivamente)
El Ranking va así:
Sospechoso:
Fichado a las: 16:09
xxxxx
08 mayo 2007
Maratón de Problemas I
Hoy empieza la Maratón de Problemas de Sospechosos Habituales. Etiquetas: matemáticas
Esta maratón de problemas está basada en la maratón de problemas que tuvo lugar ayer en la Facultad de Matemáticas y Estadística de la UPC y consistirá en una selección de los problemas que se plantearon en la mimsa.
Para participar tan sólo tienen que enviar un e-mail a sospechosos arroba gmail punto com especificando:
Pasado un día (aproximadamente) publicaré un post con la solución del problema. Tienen hasta entonces para resolverlo.
Empezaremos con un problema relativamente sencillo: Los puntos quilométricos.Un coche se desplaza a velocidad constante (diferente de 0) por una carretera. En un momento dado pasa por el punto kilométrico correspondiente a un número de dos cifras. Pasada una hora pasa por otro punto kilométrico que tiene las mismas dos cifras pero en orden inverso. Una hora más tarde pasa por un tercer punto kilométrico que vuelve a tener las dos cifras (no se especifica en que orden) pero esta vez separadas por un cero. ¿A qué velocidad iba el coche? ¿Qué puntos kilométricos recorre?
¡Suerte!
PD: Pueden usar los comentarios para pedir u ofrecer ayuda, pero procuren no destripar los problemas. Los Spoilers serán borrados.
Sospechoso:
Fichado a las: 11:45
xxxxx
07 mayo 2007
VIII Marató de Problemes
Si señores, esta tarde, si el tiempo y las autoridades lo permiten, se celebrará la VIII Marató de Problemes de la FME. Etiquetas: matemáticas
Para el que no sepa de qué va el tema ahí va un rápido resumen: Desde las 4 de la tarde y hasta que la organización se canse (que viene siendo a las 7 y pico) un puñado de valientes alumnos se enfrentarán (en grupos de 3) a unos 42 problemas. En cuanto al tipo de problema... hay de todo, geometría básica, ingenio, pensamiento lateral, álgebra, etc. Pero no se asusten, apenas es necesario conocimiento matemático alguno. Lo importante es tener ingenio y algo de práctica.
Esta ocasión es para mí, que he participado en las 7 anteriores, un tanto especial. Esta vez me ha tocado a mí seleccionar los problemas a los que se enfrentarán los pobres incautos que ya se han apuntado. Afortunadamente para ellos creo que me ha salido una Maratón demasiado fácil...
En fin, estos días estoy algo ocupado así que durante un par de semanas me dedicaré a poner un problema de la Maratón al día. Tendrán unas 20h para responder el problema vía correo electrónico a sospechosos "arroba" gmail "punto" com. Después de lo cual yo publicaré la respuesta y un nuevo problema. No olviden poner la dirección de su blog o su página personal en el mail porque haré una lista con los mejores maratonianos.
¡Suerte!
Sospechoso:
Fichado a las: 07:11
xxxxx
06 mayo 2007
Mi foto!
Esta es la foto que he enviado al grupo Flickr24h: Etiquetas: fotografía
¿Cuál es la suya?
Sospechoso:
Fichado a las: 10:40
xxxxx
05 mayo 2007
Los peligros de estudiar Bellas Artes
Vía: AutoLiniers
Sospechoso:
Fichado a las: 21:00
xxxxx
04 mayo 2007
Mañana toca foto
En Flickr han decidido montar uno de esos Pollos 2.0™ (bonitos a la par que inútiles) que tanto nos gustan a los frikis. Se trata de que todo el mundo haga fotos el día 05/05/07 (osease mañana) y las cuelgue en un grupo creado a tal efecto antes del día 21 de mayo. Etiquetas: fotografía
Vía: Sólo otro blog infame.
PD: A falta de una explicación más convincente yo creo que han escogido el día 05/05 para que no se confunda nadie con los diferentes formatos de fechas (aquí usamos el dd/mm pero en otros paises es más comun el mm/dd). Claro, que ya puestos podían haberle hecho caso al GekoNegro y hacerlo el 07/07/07 ¿no creen?
Sospechoso:
Fichado a las: 11:08
xxxxx
03 mayo 2007
Always Garfield
Picarol de Tardor me pasa un par de tiras del siempre genial Garfield: Etiquetas: humor
Garfield For President!!!
Sospechoso:
Fichado a las: 07:17
xxxxx
02 mayo 2007
Sobre el Aburrimiento
-Toni de la Torre; Dr. House, Guía para la vida- Etiquetas: citas, reflexiones, sociologíaLlenar a un ser humano de felicidad es el camino más rápido para aburrilo, hundirlo en el tedio y dejarlo en un ahogante estado de sopor depresivo. No hay nada más difícil de soportar que una serie de días buenos seguidos.
(...)
Recuerde...
La búsqueda de la felicidad no le llevará a la consecución de la felicidad.
Resto del texto en el Hombre de los Dados
[EXTRA] Hablando de aburrimiento, mirad qué ha hecho Picarol de Tardor:
Sospechoso:
Fichado a las: 16:25
xxxxx
01 mayo 2007
A raaaaaaas
Los físicos que estudian el origen del universo dicen que el Primer Segundo™ definió de una manera realmente determinante el futuro del mismo. Etiquetas: curiosidades, deporte
En ocasiones la diferencia entre el blanco y el negro, el caos y el orden, la luz y la oscuridad o la vida y la muerte es tan fina que cuesta vislumbrarla. El siguiente vídeo resulta bastante ilustrativo al respecto:
Vía: Rufadas
Sospechoso:
Fichado a las: 14:38
xxxxx
WiiDStortion.com
Etiquetas: actualidad
Aquí os la dejo por si hay alguien que como yo le gustan este tipo de cosas ;)
www.WiiDStortion.com
Sospechoso:
Fichado a las: 11:30
xxxxx
Sigue Leyendo:
Si ya has leido todos estos posts:
Cierre de Sospechosos Habituales, Breves Vacaciones, Trípode Curioso, Antoine de Saint-Exupery, Ellos nunca lo harían, Las mejores n de NaaN, Amor en HTML, Els Lladres, Tengo una (mini)falcata, 1566 revistas después, ...Puedes echarle un ojo a los casos abiertos:
Prime Number Shitting Bear, Diez Palabras, Armas Caseras, Formas de decírselo, Falacias, Relajación, El Club de la Lucha, Empezar un libro, Haikus, 21 (Solución), Profecías, 1337, Relaciones, C.I., Parecidos razonales, ROT13, N Libros, Pop-Art.Y también a estos blogs:
Oink!, Microsiervos, Escolar, Halón Disparado, Psicofonías, Las penas del Agente Smith, Sólo otro Blog Infame, Juegos de Ingenio, Gaussianos, Doblando Papeles, Curioso Pero Inútil, PJorge, La cosa húmeda, Fogonazos, Alexliam, El blog de Naan, Goshi Files, L'Última Fulla, El Hombre de los Dados.Sospechosos
- Estadísticas
- Post de Bienvenida
- La película
- Creative Commons
- Ad-Free Blogs
- Endogamy-Free
- Nuestro IBSN
- Política de Trolls
- Tagline
Participa
Archivo
- septiembre 2005
- octubre 2005
- noviembre 2005
- diciembre 2005
- enero 2006
- febrero 2006
- marzo 2006
- abril 2006
- mayo 2006
- junio 2006
- julio 2006
- agosto 2006
- septiembre 2006
- octubre 2006
- noviembre 2006
- diciembre 2006
- enero 2007
- febrero 2007
- marzo 2007
- abril 2007
- mayo 2007
- junio 2007
- julio 2007
- agosto 2007
- Posts Actuales
